Saturday, September 30, 2006
Günther's Asymmetry
Letter from Prof. Dr. Gotthard Günther to
Prof. Dr. Rainer Wiehl, from 8.12.78
"... A. Gehlen that all main culture is in principle script culture... "
"...strange, so far not solved phenomenon of the Chinese culture...in pre-Christian time admit that there are also alphabetic scripts, which can in principle be much more simple, cleared away and remained with ideograms.
In addition a further fact. There are all in all, to which also late characters excluded from taboo reasons, belong approximately 70000 ideograms. In addition however the classical north Chinese contains of only about 500 out-speakable words. In south Chinese there are perhaps 800 or 900, so that on speakable words, even if one counts only the ideograms in use, hundreds of ideogrammatic characters come.
That is, in holding to the ideograms, lies an unconscious insight of a massive asymmetry between spoken and written language.
It is the written language, on which a main culture rests.
It possesses an identity strength, which stands out clearly against the identity weakness of the spoken word. The Chinese are not in vain the socially most stable people in the past main cultures. They would not be it without this holding to a system, which seems to have disadvantages only for the progressive European.
Now the title of my work in Belgrade is "Identity and Counter-Identity" - i.e. the universe is a complexion of temporal character, in which an identity develops into a counter-identity. In doing so the universe necessarily has to pass through an epoch of ontological identity weakness.
The subjectivity of humans particularly, but generally all subjectivity, are ontological places of identity weakness, which in the long term cannot hold themselves.
That becomes understandable, if one realizes that one can exchange the words object and subject with the pair of opposites, symmetrical and asymmetrical systems. Only symmetrical systems have a certain stability.
Souls are from the beginning designed on dying, because they are expression of total asymmetry. There is no more powerful asymmetry than those, which lies in the contrast of I and world.
The Chinese failed at the role to liquidate the actual epoch of the main culture, because they tried to develop the much more powerful negative language before they possessed a positive language practically completed in Occidental mathematics.
That cannot be done for purely technical reasons, if one brings to mind oneself the beginnings of the negative language, as I indicated them in the Heidegger essay.
In this premature adherence to the ideogrammatic negative language, China swam against the current of world history, and Europe went in the opposite attitude with history." (translation, kae)
===
Decision against Alphabetism?
Gotthard Günther then asked the Sinologist Engelbert Kronthaler,
"When did the Chinese consciously decide against the introduction of alphabetic writing?"
Kronthaler answered this question some years later at 28.3.1979.
His answer was published in semiosis, 1980 in German language.
SUMMARY
"The point at issue is G. Günther´s question as to when the Chinese consciously decided in favour of visual script and against phonetic script. Alphabetical and ideogram scripts are not only various steps of development of script, they are two types, each on the pinnacle of different lines of development. The alternative phonetic script/visual script reflects the different world view of West/East, speech/script. In both, the relationship speech/script is equally evident, it is however subject to a different primacy. The conversion from the one to the other would be more than just a change of script, of apparatus, it would essentially be the change of conception, would be connected with the abandonment of the other, and would, therefore, as a whole be a reduction of complexity which must be rejected." E. Kronthaler
Chiastic Dynamism
Gunther understands the universe as a "complexion of temporal character, in which an identity develops into a counter-identity".
In contrast to the Heraklitian dynamism the Chinese dynamism is complex, parallel, concurrent, co-creative, i.e, chiastic. It is not only connected with temporality in the Western sense of linear time, but with space and spacing (making space). And this is exactly what Gunther is developing. In his lifelong search to incorporate time into logic (and arithmetic) he was forced to offer time its own space, i.e., time needs an own structural locus. Otherwise, time is ontologically subordinated to Being and Nothingness.
Loci are not in the mind (of a thinker), they are in the world. The mind is occupying only one locus in this grid of loci.
The big difference of Gunther’s approach to chiastic dynamism or dialectic cosmology to other approaches lies in the fact that he tried and partly succeeded to implement it into operative formalism. Without that it would be something like a continuation of the tradition of notional narratives.
The French philosopher Alexandre Kojeve told me, when I was driving him in West-Berlin with my Italian car to his hotel, that everything to be said had been said. The only thing to do now is to do something now. I tried to confront him with the mathematics of the Gödel proof. But this was obviously not good enough, probably because it was also only a book, again.
Next epoch
In doing so, the universe necessarily has to pass through an epoch of ontological identity weakness. Which was, after Gunther, the Western epoch.
This epoch is defined by Western philosophy, science, technology and economy based on alphabetism.
There are good reasons to think that this epoch has come to a closure.
Gunther is not saying in his letter that the next epoch will be necessarily Chinese. But he says that the Chinese thinking, mediated by its script, has an "identity strength" not existing in the Western world. But China has not (yet) developed an operativity correspondig to the complexity of its writing paradigm. This kind of operativity is proposed by the Guntherian project of a "negative language".
We shouldn't supress the thougth that a form of intelligence, not bounded and resricted by terrestrian conditions and able to communicating with human beings, would probably posses a more stable "identity strength" than any terrestrial cultures.
--
(blog-test version)
Sunday, September 24, 2006
“道可道非常道，名可名非常名”
老子《道德经》第一章说：
"道可道非常道
名可名非常名
無名天地之始有名萬物之母
故常無欲以觀其妙
常有欲以觀其徼（音：較）
此兩者 同出而異名 同謂之玄
玄之又玄 眾妙之門"
"道可道非常道，名可名非常名"，解释为"世界是可以被解释为道即规律的，但规律不是不变的；事物的概念是可以定义的，但定义不是不变的"。这是中国古代科学思想跟作为西方和现代科学技术起源的古希腊思想的根本区别。古希腊思想后来发展出了以公理化系统为特征的科学思维方法体系，公理化是形式逻辑体系的最后完成形式，是整个工业化科学技术辉煌成就的基础之一，另一个基础是系统的科学实验。
然而，后工业化的所有科学技术成就实际上是建立在两条基本科学原理之上的，而这两条原理都是关于人类认识能力的否定性的断言。
第一，海森堡的测不准原理；
第二，歌德尔的不完备定理。
第一原理是说准确地测量物理量是不可能的！第二原理是说构造完备无矛盾的体系是不可能的！这实际上是否定了工业化科学技术成就赖以建立起来的思想基础和技术基础。这又一次验证了古老的逻辑——"事物的发展本身孕育着否定自身的因素"。后工业化时代的科学技术的起点好像是从中国古代哲学家开始的地方开始的。
最重要的问题是在各个传统科学技术领域里尝试新的方法，以及开创新的科学技术领域，创建"新科学"、"新数学"。"名可名非常名"已经有了一个非常贴切的实际的例证，Python和Ruby中的变量和函数都不是预先声明的，而是在实际的应用环境中（Context/Contexture）动态地获得的，这就违背了形式逻辑的基本原测和要求！模块和软件的功能以及待要实现的任务在分布式计算环境中是被动态地分配给多个CPU处理的。
"道可道非常道
名可名非常名
無名天地之始有名萬物之母
故常無欲以觀其妙
常有欲以觀其徼（音：較）
此兩者 同出而異名 同謂之玄
玄之又玄 眾妙之門"
"道可道非常道，名可名非常名"，解释为"世界是可以被解释为道
然而，后工业化的所有科学技术成就实际上是建立在两条基本科学原
第一，海森堡的测不准原理；
第二，歌德尔的不完备定理。
第一原理是说准确地测量物理量是不可能的！第二原理是说构造完备
最重要的问题是在各个传统科学技术领域里尝试新的方法
Monday, September 18, 2006
Temporal Structures in Chinese Mathematics
Time and Methodos
The temporal structure of Chinese mathematics appears in at least two ways. One is its embedding into the well known cosmological and ontological dynamics which says the world is in a permanent change.
The second has a more a "praxeological" form and is discovered by an "ethno-methodological" approach to history. Jinmei Yuan is emphazising in her study "The role of time in the structure of Chinese logic" the double structure of temporality in the paradigm of Chinese Maths as the "now"-structure" of methodology and the dynamics of Ancient Chinese world-view.
Both should be understood as strictly different from the Greek approach of time and methodos as following a pre-given path/way.
From Ancient Greek μέθοδος (methodos) "pursuit of knowledge, investigation, mode of prosecuting such inquiry, system", from μετά, μέθ- (metα, meth-) "in the midst of, among, between, in common, along with, by aid of" + οδός (odos) "way, motion, journey".
But instead of denying the possibility of formalisms by Heraklit (panta rhei) and the dialecticians up to Hegel and dialectical materialism, the "now"-approach of Liu Hsiu shows an exciting possibility to do maths independently of axiomatics with its eternal truth and pre-given methodology (axioms+rules).
A striking similarity to the now-strategy is realized in ConTeXtures, a dynamic polycontextural programming language, I started a few years ago. The first step there is: design horizons! That means, the now tells, by analysis and experiences, situational, with which complexity and complication the method/strategy has to "start". A first sketch to model complex time-structures for programming can be found at:
www.thinkartlab.com/pkl/lola/From Ruby to Rudy.pdf
www.thinkartlab.com/pkl/lola/ConTeXtures.pdf
The question is not which philosophy mathematicians are supporting but what exactly are they doing when they are doing mathematics? Hence, how are they doing math is the question. This maybe called a "praxeological" or "ethnomethodological" approach (Garfinkel, Livingston). This, obviously, is in sharp contrast to ideology critical contemplations.
http://cseclassic.ucsd.edu/users/goguen/pps/real.pdf
A Western Summary of the Principles of Chinese Thinking
by Kaiping Peng, Richard E. NisbettPrinciple of change (Bian Yi Lu).
Chinese ways of dealing with seeming contradictions result in a dialectical or compromise approach— retaining basic elements of opposing perspectives by seeking a “middle way.” European-American ways, on the other hand, deriving from a lay version of Aristotelian logic, result in a differentiation model that polarizes contradictory perspectives in an effort to determine which fact or position is correct.
This principle holds that reality is a process. It does not stand still but is in constant flux. According to Chinese folk belief, existence is not static but dynamic and changeable. At the deepest level of Chinese philosophical thinking, "to be or not to be" is not the question because life is a constant passing from one stage of being to another, so that to be is not to be, and not to be is to be. Because reality is dynamic and flexible, the concepts that reflect reality are also active, changeable, and subjective rather than being objective, fixed, and identifiable entities.Principle of contradiction (Mao Dun Lu ).
This principle states that reality is not precise or cut-and-dried but is full of contradictions. Because change is constant, contradiction is constant. Old and new, good and bad, strong and weak, and so on, co-exist in everything.Principle of relationship or holism (Zheng He Lu)
One of the first mandatory books for literate ancient Chinese was the Yi Jing /I-Ching (The Book of Changes), in which the principle of contradiction is clearly expressed. For example, its basic theme is that the world is simply a single entity, integrated over opposites.
This principle probably constitutes the essence of dialectical thinking. It is a consequence of the principles of change and contradiction. It holds that nothing is isolated and independent, but everything is connected. If we really want to know something fully, we must know all of its relations -- how it affects and is affected by everything else. Or, to borrow a slogan from Gestalt psychology, the whole is more than the sum of its parts. Anything regarded in isolation is distorted because the parts are meaningful only in their relations to the whole, like individual musical notes embedded in a melody. [..]
The three principles of Chinese dialectical thinking are related. It is because of change that contradiction becomes inevitable; it is because change and contradiction are inevitable that it is meaningless to discuss the individual part without considering its relationships with other parts.
CULTURE, DIALECTICS, AND REASONING ABOUT CONTRADICTIONAs a Westerner I have the feeling of reading a Western compilation about Chinese thinking (world-view, logic, ontology). I will not enter this discussion because too many assumption are made which have to be questioned. Maybe, American sociologists never have heard anything in the line of Heraklit, Hegel, Marx, Piaget and other Western dialecticians. As a base for educational and political consultation it seems to me extremely blind and hegemonistic.
Kaiping Peng, Richard E. Nisbett
www-personal.umich.edu/~nisbett/cultdialectics.pdf
A discussion of the text is:
Brian Huss, Cultural differences and the Law of Noncontradiction: some criteria for further research, Philosophical Psychology, Vol. 17, No. 3, September 2004
www.tc.umn.edu/~huss0052/CPHP_17_3_03LORES.pdf
Some general informations about Cultural Geography:
http://www.apa.org/monitor/feb03/intelligence.html?
Brian Huss:
It is extremely difficult to provide a non-circular justification for the LNC (Law of Non-Contradiction), and yet the LNC seems to act as a basic standard for reasoning in the West. If non-Western cultures do not believe the LNC holds, then meaningful cross-cultural discussion and debate will be very difficult, to say the least. In this paper it is argued that the distinction between belief and acceptance is important in analyzing cross-cultural studies on the way people reason. [...] The distinction between belief and acceptance is used to demonstrate that the empirical data currently available fail to show that the LNC is not a universal of folk epistemology.
Thus, I will start with only one simple question.
Obviously, my question will not deal with the problem if there is a contradiction for a Chinese farmer to be or/and not to be in the possession of $1000.-
What do we mean with "contradiction" (矛盾)?
I remember reading German, French and English translations of Mao Tse Tung’s study "On Contradiction". Most of his examples showed me that the term "contradiction" is misleading. The examples for contradiction are: polar, opposite, antagonism, struggle, etc. and logical contradiction was only a part of it.
"Contradiction and struggle are universal and absolute, but the methods of resolving contradictions, that is, the forms of struggle, differ according to the differences in the nature of the contradictions. Some contradictions are characterized by open antagonism and others are not. In accordance with the concrete development of things, some contradictions, which were originally non-antagonistic, develop into antagonistic ones, while others which were originally antagonistic develop into non-antagonistic ones."Mao's explanation is not easy to accept for non-dialecticians. First for Western philosophy and science there are no contradiction in the univere at all. Second, Mao's definition is in itself contradictionous. If contradictions are "universal and absolute", how do we have to understand the "but"? And the "absolute and universal" is changing all the time? Contradiction as a self-referential term, but not in Aristotelian logic. Neither in paraconsistent logics.
"On Contradiction" (August 1937), Selected Works, Vol. I, p 344.
http://www.rrojasdatabank.org/mao11.htm
Then I learnt that the Chinese ideogram for contradiction, 矛盾, has absolutely nothing to do with the latin dictio and contra-dictio (speech and contra-speech). But about spear (矛)+shield (盾). Later I was told that there are not only two fighters with their spear+shield in a fighting position, but that the ideogram goes back to the hieroglyphs for sun and moon.
Not only that we are far away from any phono-logical terms of contradicting and contradiction with its logos-based duality of true and false, the structure of a fight between two fighters is not dual but 4-fold: 2 positions with spear+shield, i.e. in fact, spear vs. shield + shield vs spear.
And this is exactly the chiastic structure of change. Thus, change is not a simple continous floating Heraklitian flux but an interplay between different qualities.
In other words, the 3 principles mentioned above appear as a complex interacting pattern; "contradiction" and "change" are "one". Hence, the "speech act" of contradicting in a opponent/proponent game is a very small and specific layer, (for lawyers at court), of a "shield-盾+spear-矛"-interaction.
Therefore, I very much prefer the approach of studying what exactly Ancient Chinese mathematician did when the practised mathematics.
An important step to this kind of studies is done by Jinmei Yuan.
http://ccbs.ntu.edu.tw/FULLTEXT/JR-JOCP/jc106031.pdf
The Jinyou-Strategy of Chinese Math
"Chinese logicians in ancient times presupposed no fixed order in the world. Things are changing all the time. If this is true, then universal rules that aim to represent fixed order in the world for all time are not possible."This sounds familiar to Heraklitian philosophy and the Western understanding of Chinese world-view. But suddendly there is something surprisingly different:
"Chinese logical reasoning instead foregrounds the element of time as now. Time, then, plays a crucial role in the structure of Chinese logic."Because of the "mutual relations" and "bi-directional" structure of Chinese strategies I think the time mode of "now" is not the Western "now" appearing in the linear chain of "past–present–future". To understand "now" in a non-positivist sense of "here and now" it could be reasonable to engage into the adventure of reading Heidegger’s and Derrida’s contemplation about time. This seems to be confirmed by the term "happenstance" (Ereignis) which is crucial to understand the "now"-time structure.
The praxeological analysis discovers the patterns of "problem solving" before/beyond axiomatic deductions, i.e., beyond the linear pathway from problem to solution under an invariable method.
"To uncover the logical structure and presumption in Chinese mathematical art, I would like, first of all, to call attention to a few important and interesting features of the Nine Chapters:Jinmei Yuan's comment
1. None of the mathematical terms in the Nine Chapters have a given definition.
2. No demonstrations between a given problem and an answer are offered.
3. The 246 problems in the Nine Chapters mostly begin with the phrase Jinyou, which means “Now, there is . . .”
Jinyou is a general way to form patterns in the Nine Chapters.
Second, I would like to briefly summarize the patterns according to which the mathematical problems in the Nine Chapters are organized:
Pattern 1:
Now, there is ( jinyou) . . . Tell (qiu):
Answer (da):
Art/Method (shuyue):
Pattern 2:
The name of an art/method (shu) or a rule (fa)
Art/Method (shuyue):
Now, there is ( jinyou) . . . Tell (qiu):
Answer (da):
Art/Method (shuyue)
Pattern 3:
Now, there is ( jinyou) . . . Tell (qiu):
Answer:
Art/Method:
Another art/method:
Another art/method:
Another art/method:
The first phrase here is “Now, there is . . .” ( jinyou).The relevance of happenstance (Ereignis)
If one takes a close look at the above pattern, one can easily see that “time” plays an important role in each mathematical problem-solving procedure. Almost all of the problems in the Nine Chapters start with the assumption, “Now, there is . . .” (jinyou), which is a good starting point for us to explore the logical space in these patterns.
To the extent that the time, “now” ( jin), is involved, the problems in which Chinese mathematicians are interested are particular ones, such as those that arise during a face-to-face conversation in the present.
In other words, Chinese logical space is structured in the time, “now.” Chinese people are only concerned with the logical relations that exist in the present practice, not something beyond the present time, such as “universal truth.”
"The phrase jinyou is crucially important to understanding the patterns in the Nine Chapters. Having discussed the role of time, the now ( jin), in the patterns, the meanings of you in the phrase of “now, there is . . .”
(jinyou) should be clarified.
The character you in Chinese means that a happenstance exists or shows itself, or that something is possessed. The original character you is written in such a way that the top part is a hand and the bottom part is a moon.
In the Shuo Wen, an early Chinese lexicon, Xu Shen says, “You is the thing that does not always exist. Spring and Autumn has an explanation: [for example,] the happenstance of a solar eclipse or lunar eclipse.”
It is clear that you in the Nine Chapters does not hold the meaning of something that is given by mathematicians theoretically, but that it means a concrete problem that occasionally exists as a special event, in a particular time and space."Happenstance is the meeting between two strangers who have never met before, normally in a completely random situation."
If one holds the presumption that there is a fixed order in this world and that things have their stable positions, then the notion of “given a problem” or “given a rule” can make sense in mathematical reasoning."
http://en.wikipedia.org/wiki/Happenstance
Jinmei Yuan concludes
"Chinese mathematical art aims to clarify practical problems by examining their relations; it puts problems and answers in a system of mutual relation—a yin-yang structure for all the things in a changing world. The mutual relations are determined by the lei (kind), which represents a group of associations, and the lei (kind) is determined by certain kinds of mutual relations."
Sunday, September 17, 2006
中国数学中的构造主义...
中国古代数学不是基于形式逻辑的,而是基于一种构造主义、操作主义和组合学的，更重要的是对对象的位置操作，要发现一个幻方，就像是操作一个置换群一样。这点跟古希腊完全不同。
將1 ~ 9 填入下方九個方格中，使得每行、每列及對角線之和皆相等。這就是著名的魔方陣了。
那麼要怎麼做呢？根據楊輝《續古摘奇算經》（1275年）的紀載，
九子斜排 上下對易 左右相更 四維挺進
戴九履一 左三右七 二四為肩 六八為足
接下來則是
這就是楊輝魔方陣的原理了，如果按照現在的解釋應做如是想法：
1.求出這個共同的和是多少？
1 + 2 + 3 +‧‧‧+ 9 ﹦45
45 ÷3 ﹦15
2.決定中間那格為何數？為何是5？
1 ~ 9中，任取三數相加為15有八種情況：
1 + 5 + 9 ﹦15 2 + 5 + 8 ﹦15
3 + 5 + 7 ﹦15 4 + 5 + 6 ﹦15
2 + 4 + 9 ＝15 3 + 4 + 8 ＝15
1 + 6 + 8 ＝15 2 + 6 + 7 ＝15
在 這八種情況中5出現四次，2、4、6、8各出現三次， 1、3、7、9各出現二次，對應到方格，我們發現中間那格共有1行1列及兩對角線通過四個角落各有1行1列及一對角線通過剩餘四格僅有1行1列通過所以將 5填入中間那格，2、4、6、8填入四個角落 (2、5、8成一直線or 4、5、6成一直線)
再將1、3、7、9填入適當的剩餘四格中．
將1 ~ 9 填入下方九個方格中，使得每行、每列及對角線之和皆相等。這就是著名的魔方陣了。
那麼要怎麼做呢？根據楊輝《續古摘奇算經》（1275年）的紀載，
戴九履一 左三右七 二四為肩 六八為足
| 九子斜排 | 上下對易 | 左右相更 | 四維挺進 |
 |  |  |  |
接下來則是
| 戴九履一 左三右七 二四為肩 六八為足 | |
這就是楊輝魔方陣的原理了，如果按照現在的解釋應做如是想法：
1.求出這個共同的和是多少？
1 + 2 + 3 +‧‧‧+ 9 ﹦45
45 ÷3 ﹦15
2.決定中間那格為何數？為何是5？
1 ~ 9中，任取三數相加為15有八種情況：
1 + 5 + 9 ﹦15 2 + 5 + 8 ﹦15
3 + 5 + 7 ﹦15 4 + 5 + 6 ﹦15
2 + 4 + 9 ＝15 3 + 4 + 8 ＝15
1 + 6 + 8 ＝15 2 + 6 + 7 ＝15
在 這八種情況中5出現四次，2、4、6、8各出現三次， 1、3、7、9各出現二次，對應到方格，我們發現中間那格共有1行1列及兩對角線通過四個角落各有1行1列及一對角線通過剩餘四格僅有1行1列通過所以將 5填入中間那格，2、4、6、8填入四個角落 (2、5、8成一直線or 4、5、6成一直線)
再將1、3、7、9填入適當的剩餘四格中．
Saturday, September 16, 2006
Beyond Fears and Denials
Why should we be inspired by ancient number theory?
Today, it is nearly impossible to imagine another paradigm of numbers than what we are taught at school and are experiencing in everyday life. But also academic mathematical studies of number theory, despite its enormous complexity, is based on the classic concept of natural numbers. It is not well known that even proper axiomatizations of the system of natural numbers (Peano Arithmetic) have failed to characterize the system of natural numbers up to concreteness. Despite of the conceptual gaps left, there are no serious attempts to liberate the concept of natural numbers from its modern historical determination as a series of linear ordered elements. There exist many logical systems, different to classic logic, but more or less no arithmetical systems which could be considered as non-classic (heterodox, deviant, alternative, etc.) like the logical systems.
Refutation by fear
There are only a very few attempts to develop radically new ways of thinking and computation. One of such an exception is given by the work of the philosopher and cybernetician Gotthard Gunther. He stated that his experiences shows him that there is a deep existential and emotional defence in Occidental thinking to accept an involvement into new thoughts concerning the foundations of logic and arithmetic and mathematics. Such new thoughts are not proven wrong but are simply rejected and denied by the fear to face and encounter new and unknown possibilities of thinking. Also such projects may be rooted in attempts of a new understanding and interpretation of Ancient experiences and knowledge, the emotional refutation is irreconcilable.
Thus, a historical understanding of the development and limits of our thinking in science and technology could be of help. World-views and paradigms of thinking appear to be enclosed by historical epochs. In his propaganda of global revolution, Joseph Stalin made it clear that their is a holy exception: mathematical sciences are neutral, i.e. class and history independent, especially mathematics of numbers. With logic, the case was more difficult because of the dialectics of Hegel/Marx. But there was a clear cleansing too: dialectics are beyond any formalism.
Today, there will even a math-gene be found and some math-neurons proving the inherent and innate natural human character of arithmetic and logic. Others will conceive a more spiritual explanation.
James R Hurford, The Neural Basis of Predicate-Argument Structure
http://www.ling.ed.ac.uk/~jim/newro.htm
Few new approaches
Nevertheless, new approaches are appearing, more or less despite academic prohibitions, in mathematical sciences, trying to surpass the monocontexturality of classical thinking: polycontexturality (Gunther), ultra-intuitionism (Yessenin-Volpin), poly-mathematics (Arnold) and the idea to a theory of n-categories (Baez). But all those attempts are grammatologically based on a classic understanding of semiotics and its alphabetism. The only exception I know, is proposed by the few sketches of Gunther’s kenogrammatics.
Transitions from Pythagoras to Aristotle and back?
has done proper work in cleaning up the scenario. Even today it is dificult to understand his trick: his refutations are based on a logic he just introduced. A logic which in its restriction has no applicability and reasonability for the Ancient paradigm of thinking. Thus, to show a contradiction in Pythagorean number theory is simply a red herring. Figurative numbers have successors and – neighbors. But that is utter nonsense if we just have postulated the principle of linearity of natural numbers.
There is not much written evidence from Pythagoras, he even cultivated "deep silence", meditation. In his powerful and detailed denial, Aristotle has drawn a picture of Pythagoreanism we can read now in two directions: pro-Pythagorean and pro-Aristotelian.
enter: Aristotle, Metaphysics, book XII, XIII.
http://www.britannica.com/eb/art-75247
Aristotle's trickery
Pythagorean aritmetic insisted on the systematic exclusivenes of the number four, used in their technique of the Tectractis ("counting by the principle of four"). It can only be a bad joke of Aristotle to presume that the Pythagoreans could not calculate further than to the number four. Because he has known this was wrong he constructed a logical contradiction in the Pythagorean number theory between the finitenes of the Tectractis and the infinitenes of counting numbers; simply by presuming that both number systems must be identical. He didn't accept the difference between counting numbers and Pythagorean conceptual category numbers as scientifically relevant. With this voluntary decision, for which there is no proof, he introduced the principle of the uniqueness of the serie of natural numbers. Today, we are restricted to the conceptual number two: dualism, binarism, digitalism, two-valuedness, etc. But this seems not to be a restriction but a taboo.
The revolution happend for general economic reasons. Its justification was given by its general success. Today we are trapped in this paradigm which has started to turn against its own legitimation. It's time to study the transition which established Aristotelian thinking. Its merits and its sacrifices.
Pluri-dimensionality
Figurative numbers are finite, qualitative, cosmic and related to the soul.
Mathematical numbers are infinite, formal and related to empirical reality. Figurative numbers are pluri-dimensional, arithmetic numbers are one-dimensional.
Thus, in what exactly is such a profound fear rooted?
The deep fear, expressed by many scholars and politicians, is this: if we abandon the principles of linearity and hierarchy in arithmetic, logic, deduction and computation we end in chaos. That is, we naturally will lose our human dignity. Positively, this situation is collected in a beautiful text by Philip Wadler.
Whatever it may be.
Even if this world-view may be ultimate, universal and natural for human thinking, today, we are in big troubles with its narrowness and limited conception of hierarchic thinking and computing.
One serious fear to leave the paradigm of linearity and hierarchy for formal and opperative reasoning and computation is the believe that the only alternativity to linearity is circularity. And circularity is not only produc
ing antinomies and paradoxes but was the pattern of Ancient, non-operative thinking. The fear is well justified. "Circular" thinking brought it up to the informational feedback loops of Cybernetics and to its "post-modern" version of Second-Order Cybernetics with its metaphor of Uroboros and criculus creativus. But not to a working new paradigm of hard science. The opposite or complementarity to hierarchy is not given by a simple regression to circularity but needs a complex interplay between hierarchies and heterarchies. Such an interplay can not adequately be represented by a singular metaphor or model. Its realizations are embedded in the dynamics of an interacting complementarity of metaphors, models, paradigms of conceptualization and computation not accessible to classic scientific thinking.
Computing paradigm for the 21st century
Problems of interactivity and reflectionality of computing systems are not covered by classic models of computation like Turing Machines. Such a paradigm is modeled along the line of calculation and algorithms. Both are closed systems without any interaction and reflection while computing. Obviously, they are based on the linearity of the arithmetic of natural numbers, or more generally on the linearity of algorithmic sign systems, i.e. formal (programming) languages.
But, say, the Internet is not an algorithmic problem solving system. Locally, there are many programs solving specific problems, but the system as a whole, globally, it is not solving a single problem. It is an interactional service system – without beginning nor ending.
Peter Wegner is emphazising this new situation and has developed important work to its conceptionalization. A new distinction is introduced: abstract algorithmical computation vs. empirical situational interaction.
Chances to learn from the past
Citations from: Jinmei Yuan, Exploring the logical space in the patterns of classical Chinese mathematical art.
"The beauty of Chinese mathematical arts is, to some degree, similar to the beauty of poetry; it requires the participation of subjects."
"Chinese people are only concerned with the logical relations that exist in the present practice, not something beyond the present time, such as “universal truth.”"
"The logical reasoning of kind (lei) can be described as a net, which represents the main characteristic of Chinese logic."
"My standpoint is that Chinese mathematicians’ reasoning was based on a very different presumption. The presumption in the Euclidean tradition is that there is a fixed order in this world, and the goal of doing mathematics is to represent the beauty of this rational order. The presumption of the Chinese mathematicians is that there is no fixed order in this world. For them, things are changing all the time. Following this presumption, any universal rule, which aims to represent the fixed order in the world, is not important, or for that matter, even impossible. The mathematical art in Chinese culture is akin to conversational reasoning."
"The logic that Chinese mathematicians followed in this kind of conversational reasoning deals with the relations among particulars in present practice. The aim of this kind of reasoning is to represent the harmony of relations among particulars at the moment." Jinmei Yuan
http://ccbs.ntu.edu.tw/FULLTEXT/JR-JOCP/jc106031.pdf
To teach Chinese students Aristotle can have a double function: to learn about the world-view of Western logic, ontology, semiotics, etc. and to learn against which Ancient thinking it was established and which means had been developed to do it. It could be an exiting possibility to compare Pythagoreanism with Ancient Chinese thinking. Grammatologically, both are not based in the medium of alphabetism.
Today, it is nearly impossible to imagine another paradigm of numbers than what we are taught at school and are experiencing in everyday life. But also academic mathematical studies of number theory, despite its enormous complexity, is based on the classic concept of natural numbers. It is not well known that even proper axiomatizations of the system of natural numbers (Peano Arithmetic) have failed to characterize the system of natural numbers up to concreteness. Despite of the conceptual gaps left, there are no serious attempts to liberate the concept of natural numbers from its modern historical determination as a series of linear ordered elements. There exist many logical systems, different to classic logic, but more or less no arithmetical systems which could be considered as non-classic (heterodox, deviant, alternative, etc.) like the logical systems.
Refutation by fear
There are only a very few attempts to develop radically new ways of thinking and computation. One of such an exception is given by the work of the philosopher and cybernetician Gotthard Gunther. He stated that his experiences shows him that there is a deep existential and emotional defence in Occidental thinking to accept an involvement into new thoughts concerning the foundations of logic and arithmetic and mathematics. Such new thoughts are not proven wrong but are simply rejected and denied by the fear to face and encounter new and unknown possibilities of thinking. Also such projects may be rooted in attempts of a new understanding and interpretation of Ancient experiences and knowledge, the emotional refutation is irreconcilable.
Thus, a historical understanding of the development and limits of our thinking in science and technology could be of help. World-views and paradigms of thinking appear to be enclosed by historical epochs. In his propaganda of global revolution, Joseph Stalin made it clear that their is a holy exception: mathematical sciences are neutral, i.e. class and history independent, especially mathematics of numbers. With logic, the case was more difficult because of the dialectics of Hegel/Marx. But there was a clear cleansing too: dialectics are beyond any formalism.
Today, there will even a math-gene be found and some math-neurons proving the inherent and innate natural human character of arithmetic and logic. Others will conceive a more spiritual explanation.
James R Hurford, The Neural Basis of Predicate-Argument Structure
http://www.ling.ed.ac.uk/~jim/newro.htm
Few new approaches
Nevertheless, new approaches are appearing, more or less despite academic prohibitions, in mathematical sciences, trying to surpass the monocontexturality of classical thinking: polycontexturality (Gunther), ultra-intuitionism (Yessenin-Volpin), poly-mathematics (Arnold) and the idea to a theory of n-categories (Baez). But all those attempts are grammatologically based on a classic understanding of semiotics and its alphabetism. The only exception I know, is proposed by the few sketches of Gunther’s kenogrammatics.
Transitions from Pythagoras to Aristotle and back?
"The access to pluri-dimensionality and to a delinearized temporality is not a simple regression toward the "mythogram"; on the contrary, it makes all the rationality subjected to the linear model appear as another form and another age of mythography.The ultimate cultural revolution which happened in Ancient Greece was the strict separation of the numbers as figurative, geometric, speculative, esoteric, thus Ancient, and numbers as ordinary objects of calculation and contemplation in science and the empirical, economic world, thus modern. The ancient Pythagorean approach was denounced as archaic and mythical. Not suitable for calculation. Aristotle
The meta-scientificity which are thus announced within the meditation upon writing can therefore be no more shut up within a science of man than conform to the traditional idea of science. In one and the same gesture, they leave man, science, and the line behind." Jaques Derrida, Of Grammatology, p.84
has done proper work in cleaning up the scenario. Even today it is dificult to understand his trick: his refutations are based on a logic he just introduced. A logic which in its restriction has no applicability and reasonability for the Ancient paradigm of thinking. Thus, to show a contradiction in Pythagorean number theory is simply a red herring. Figurative numbers have successors and – neighbors. But that is utter nonsense if we just have postulated the principle of linearity of natural numbers.There is not much written evidence from Pythagoras, he even cultivated "deep silence", meditation. In his powerful and detailed denial, Aristotle has drawn a picture of Pythagoreanism we can read now in two directions: pro-Pythagorean and pro-Aristotelian.
enter: Aristotle, Metaphysics, book XII, XIII.
http://www.britannica.com/eb/art-75247
Aristotle's trickery
Pythagorean aritmetic insisted on the systematic exclusivenes of the number four, used in their technique of the Tectractis ("counting by the principle of four"). It can only be a bad joke of Aristotle to presume that the Pythagoreans could not calculate further than to the number four. Because he has known this was wrong he constructed a logical contradiction in the Pythagorean number theory between the finitenes of the Tectractis and the infinitenes of counting numbers; simply by presuming that both number systems must be identical. He didn't accept the difference between counting numbers and Pythagorean conceptual category numbers as scientifically relevant. With this voluntary decision, for which there is no proof, he introduced the principle of the uniqueness of the serie of natural numbers. Today, we are restricted to the conceptual number two: dualism, binarism, digitalism, two-valuedness, etc. But this seems not to be a restriction but a taboo.
The revolution happend for general economic reasons. Its justification was given by its general success. Today we are trapped in this paradigm which has started to turn against its own legitimation. It's time to study the transition which established Aristotelian thinking. Its merits and its sacrifices.
Pluri-dimensionality
Figurative numbers are finite, qualitative, cosmic and related to the soul.
Mathematical numbers are infinite, formal and related to empirical reality. Figurative numbers are pluri-dimensional, arithmetic numbers are one-dimensional.
"Thus peculiar dialectic situation is produced for the earthly thinker. He has the choice of interpreting the Peano sequence of numbers as an ultimate dilution of the orders of esoteric numbers to a degree where they become unfit for the representation of philosophic problems and where they are only good for showing money amounts in cash registers or temperature grades on the scales of thermometers and for similar trivial tasks. But we can also look at them as the material from which we build up orders of esoteric numbers starting from systems with minimal complexity to ever increasing structures of higher order. This produces a scale that proceeds from finitude to finitude! An infinite system of esoteric numbers is inconceivable. If trying to think it we cannot help but apply the numbers of the Peano sequence - which means: we drop out of the realm of metaphysics." Gotthard Gunther, Number and Logos
Thus, in what exactly is such a profound fear rooted?
The deep fear, expressed by many scholars and politicians, is this: if we abandon the principles of linearity and hierarchy in arithmetic, logic, deduction and computation we end in chaos. That is, we naturally will lose our human dignity. Positively, this situation is collected in a beautiful text by Philip Wadler.
"Whether a visitor comes from another place, another planet, or another plane of being we can be sure that he, she, or it will count just as we do: though their symbols vary, the numbers are universal. The history of logic and computing suggests a programming language that is equally natural. The language, called lambda calculus, is in exact correspondence with a formulation of the laws of reason, called natural deduction. Lambda calculus and natural deduction were devised, independently of each other, around 1930, just before the development of the first stored program computer. Yet the correspondence between them was not recognized until decades later, and not published until 1980. Today, languages based on lambda calculus have a few thousand users. Tomorrow, reliable use of the Internet may depend on languages with logical foundations."Was Pythagoras and the Ancient Chinese mathematicians, to mention only this two, pre-humans? And would we fall back to a pre-human level of consciousness if we would give up to believe in the ultimate universality of mono-contexturality? Or do we have to transmute to trans-humans, or even to a Übermensch (super-human) like in Nietzsches Zarathustra? This, with involving all the theological hybris?
http://homepages.inf.ed.ac.uk/wadler/topics/history.html#drdobbs
More at: http://www.thinkartlab.com/pkl/media/SUSHIS_LOGICS.pdf
Whatever it may be.
Even if this world-view may be ultimate, universal and natural for human thinking, today, we are in big troubles with its narrowness and limited conception of hierarchic thinking and computing.
One serious fear to leave the paradigm of linearity and hierarchy for formal and opperative reasoning and computation is the believe that the only alternativity to linearity is circularity. And circularity is not only produc
ing antinomies and paradoxes but was the pattern of Ancient, non-operative thinking. The fear is well justified. "Circular" thinking brought it up to the informational feedback loops of Cybernetics and to its "post-modern" version of Second-Order Cybernetics with its metaphor of Uroboros and criculus creativus. But not to a working new paradigm of hard science. The opposite or complementarity to hierarchy is not given by a simple regression to circularity but needs a complex interplay between hierarchies and heterarchies. Such an interplay can not adequately be represented by a singular metaphor or model. Its realizations are embedded in the dynamics of an interacting complementarity of metaphors, models, paradigms of conceptualization and computation not accessible to classic scientific thinking.Computing paradigm for the 21st century
Problems of interactivity and reflectionality of computing systems are not covered by classic models of computation like Turing Machines. Such a paradigm is modeled along the line of calculation and algorithms. Both are closed systems without any interaction and reflection while computing. Obviously, they are based on the linearity of the arithmetic of natural numbers, or more generally on the linearity of algorithmic sign systems, i.e. formal (programming) languages.
But, say, the Internet is not an algorithmic problem solving system. Locally, there are many programs solving specific problems, but the system as a whole, globally, it is not solving a single problem. It is an interactional service system – without beginning nor ending.
Peter Wegner is emphazising this new situation and has developed important work to its conceptionalization. A new distinction is introduced: abstract algorithmical computation vs. empirical situational interaction.
"The interaction paradigm provides a new conceptualization of computational phenomena that emphasizes interaction rather than algorithms. The recognition that these characteristics are inherently outside the traditional conceptualization of computation is the basis for this new paradigm for computing, built around the unifying concept of interaction. Concurrent, distributed, reactive, embedded, component-oriented, agent-oriented and service-oriented systems all exploit interaction as a fundamental paradigm.With such an interactional approach, referring to situational real world events, like "driving home from work", problems of formalization beyond classic abstract algorithms are arising. But modeling the intuition of the new situation is not yet delivering a working formalism for computation. Interactional computation as a new empirical paradigm needs a mathematical framework which is surpassing the limits of encapsulated linearity. Maybe we should understand that Ancient number theory, Pythagorean and Chinese, is positioned before the distinction of formal/material, abstract/empirical, subjective/objective and computable/non-computable. Such a pre-/trans-scientific paradigm would involve, from the very beginning, interactional subjectivity into the game of its formalisms and operativity.
Peter Wegner’s claim (CACM, May 1997) that “interaction is more powerful than algorithms” challenges our fundamental assumptions about the nature of computation and the notion of computational problems, reinterpreting the Church-Turing thesis without attacking it directly. This claim is an open invitation to researchers to develop models, tools, and methods that can lend credence to it. Since then, pervasive/ubiquitous computing – which epitomizes interaction – has been proposed as the leading computing paradigm for the 21st century."
http://www.cse.uconn.edu/cse/finco05/#panel
Chances to learn from the past
"The author himself confesses that if somebody - before he had the good fortune of knowing McCulloch - had suggested that in Metaphysics we require numbers in order to understand ideas instead of saying that ideas are necessary to understand numbers he would have more or less politely changed the topic.Was Pythagoras Chinese?
It took a McCulloch to show him that it had been the tragic fate of Western civilization to permit the concept of the idea to gain metaphysical precedence before number and that from this very choice the fateful split between sciences and the humanities had resulted." Gotthard Gunther, Number and Logos
Citations from: Jinmei Yuan, Exploring the logical space in the patterns of classical Chinese mathematical art.
"The beauty of Chinese mathematical arts is, to some degree, similar to the beauty of poetry; it requires the participation of subjects."
"Chinese people are only concerned with the logical relations that exist in the present practice, not something beyond the present time, such as “universal truth.”"
"The logical reasoning of kind (lei) can be described as a net, which represents the main characteristic of Chinese logic."
"My standpoint is that Chinese mathematicians’ reasoning was based on a very different presumption. The presumption in the Euclidean tradition is that there is a fixed order in this world, and the goal of doing mathematics is to represent the beauty of this rational order. The presumption of the Chinese mathematicians is that there is no fixed order in this world. For them, things are changing all the time. Following this presumption, any universal rule, which aims to represent the fixed order in the world, is not important, or for that matter, even impossible. The mathematical art in Chinese culture is akin to conversational reasoning."
"The logic that Chinese mathematicians followed in this kind of conversational reasoning deals with the relations among particulars in present practice. The aim of this kind of reasoning is to represent the harmony of relations among particulars at the moment." Jinmei Yuan
http://ccbs.ntu.edu.tw/FULLTEXT/JR-JOCP/jc106031.pdf
To teach Chinese students Aristotle can have a double function: to learn about the world-view of Western logic, ontology, semiotics, etc. and to learn against which Ancient thinking it was established and which means had been developed to do it. It could be an exiting possibility to compare Pythagoreanism with Ancient Chinese thinking. Grammatologically, both are not based in the medium of alphabetism.
Monday, September 11, 2006
Negative Ecology of Sign Systems
Die Ressourcen des Denkens
Das Denken vollzieht sich im Medium des Zeichengebrauchs. Die Semiotik als formalisierte Theorie des rationalen Zeichengebrauchs kennt nur die abstrakte Verknüpfung (Konkatenation/Substitution) von vorgegebenen Zeichen eines (beliebigen, endlichen oder unendlichen) Zeichenrepertoires, das allerdings formal auf zwei Elemente (Atomzeichen und Leerzeichen) reduziert werden kann. Das Zeichen als Zeichengestalt trägt sich im Denken aufgrund der Trägerfunktion der Materialität des Zeichenereignisses. Die Differenz von Zeichengestalt und Zeichenvorkommnis kommt in der Semiotik selbst nicht zur Darstellung; sie ist ihre verdeckte Voraussetzung.
Die Zeichengestalt verbraucht sich nicht im Gebrauch ihres Ereignisses. Der Modus der Wiederholung des Zeichens ist abstrakt und gründet sich auf der Abwesenheit des Subjekts und der Annahme der Unendlichkeit der Ressourcen (Raum, Zeit, Materie).
[...]
Der Alphabetismus findet in seiner letztlichen Digitalität und Linearität multimedial zu sich selbst und zu seinem Abschluß in der Objektivation seiner vermeintlichen Vernetzung. Die Graphematik be-wegt den Übergang der Inskription zur Ermöglichung einer nach-schriftlichen und trans-terrestrischen Epoche des Welt-Spiels.
Kaehr, Proömik und Disseminatorik, 1995
Translation
Thinking is realizing itself in the medium of the use of signs. Semiotics as the formalized theory of rational use of signs knows only the abstract linkage (concatenation/substitution) of given signs (finite or infinite) of a sign repertoire, which however can be formally reduced to two elements (atomic sign and blank) only.
In thinking, the sign as sign type carries itself due to the carry function of the materiality of the event of sign tokens. The difference of sign type and sign token (occurrence) itself is not reflected in semiotics; it is its covered condition.
The sign type does not use (consume) itself in the use of its event. The mode of iterability of the signs is abstract and based on the absence of subjectivity and the assumption of the infinity of resources (space, time, matter).
About sign systems
Elementary signs
„Elementary signs are signs that we shall consider as not having parts. The content of this concept depends upon the conventions that are assumed. [..] In simultanous consideration of any two elementary signs, we determine whether they are the same or different. These concepts are also conditional."
Abstraction of identification
"The possibility of determining when two elementary signs are the same permits us, applying an abstraction of identification, to speak of two identical elementary signs or of one and the same elementary sign. On this basis, we introduce the concept of an abstract elementary sign, that is, of an elementary sign, considered up to identity.
Concrete elementary signs will be considered as representatives of the corresponding abstract elementary signs. Two concrete elementary signs represent one and the same abstract elementary sign if and only if they are identical."
Abstract alphabets
"Lists of elementary signs are called alphabets. We shall call two alphabets equal if every elementary sign appearing in the first alphabet is identical with a certain elementary sign appearing in the second alphabet, and conversely. Alphabets considered up to equality will be called abstract alphabets."
Potential realizability
"Another abstraction, (...), is abstraction of potential realizability. This consists in departing from real limits of our constructive possibilities and beginning to discuss arbitrarily long abstract words as if they were constructible. Their realizability is potential: their representatives could be practically realized if we had at our disposal sufficient time, space, and materials." A. A. Markov
Ideality of Notational Systems
The abstractness of sign systems and their independence of real world conditions like space and matter, are brought one step further by Alfred Goguen’s definition of institutions and signatures for programming languages.
To speak about alphabetism in formal systems, with its atomicity, linearity, iterability, and ideality is not forgetting the conceptual move from alphabets as sign repertoires to the more abstract, category theoretic concept of signatures of institutions.
"Institutions accomplish this formalization by passing from "vocabularies" to signatures, which are abstract objects, and from "translations among vocabularies" to abstract mappings between objects, called signature morphisms;
then the parameterization of sentences by signatures is given by as assignment of a set Sen(S) of sentences to each signature S, and a translation Sen(f) from Sen(S) to Sen(S') for each signature morphism f: S –-> S', while the parameterization of models by signatures is given by an assignment of a class Mod(S) of models for each signature S, and a translation Mod(S') –-> Mod(S) for each f: S –-> S'.
[...]
Satisfaction is then a parameterized relation |=S between Mod(S) and Sen(S), such that the following satisfaction condition holds, for any signature morphism f: S –-> S', any S-model M, and any S'-sentence e: M |=S f(e) iff f(M) |=S' e
This condition expresses the invariance of truth under change of notation."
http://www.cs.ucsd.edu/users/goguen/projs/inst.html
Signatures are even better realizing alphabetism than sign repertoires because they are emphasizing the abstractness of alphabetical signs, that is, the ideality of signs, and sign systems, in contrast to the concrete occurrence of signs, independent of the content of the sign repertoire, i.e., the concrete notational material. Sign systems are not only characterized by atomicity, linearity, iterability, but also by ideality. Ideality is the medium of the realization of signs.
Uniqueness of Semiotics
Despite the fact that semiotics, like institutions, have many realizations, they are conceived as being conceptually unique. There is, in principle, one and only one semiotics. As there is, in principle, one and only one (u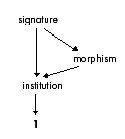
niversal) logic. There may be many different semiotic or logical systems realizing special purposes.
In the conceptual graph, uniqueness (oneness) is marked as 1. The trichotomy of semiotics is ruled by the order relations between alphabet (signature), rules (morphisms) and semiotics (institution) based on 1.
The oneness of semiotics has its foundation in mono-contexturality as opposed to poly-contexturality.
Negative Ecology
Today, we have to consider the destructiveness of sign systems. Technology, as realized in computing, is based on a sign-economy which is denying the limitations of its resources. By the application to real-world problems of understanding, organizing and computation, the abstractness of sign systems has become, after its deliberating function to human society, more and more an ecologically exploitative and destructive power. This might be a historical situation and might not to be the final paradigm of scriptural work. New notational systems, beyond alphabetism and not based on uniqueness, have to be invented.
Das Denken vollzieht sich im Medium des Zeichengebrauchs. Die Semiotik als formalisierte Theorie des rationalen Zeichengebrauchs kennt nur die abstrakte Verknüpfung (Konkatenation/Substitution) von vorgegebenen Zeichen eines (beliebigen, endlichen oder unendlichen) Zeichenrepertoires, das allerdings formal auf zwei Elemente (Atomzeichen und Leerzeichen) reduziert werden kann. Das Zeichen als Zeichengestalt trägt sich im Denken aufgrund der Trägerfunktion der Materialität des Zeichenereignisses. Die Differenz von Zeichengestalt und Zeichenvorkommnis kommt in der Semiotik selbst nicht zur Darstellung; sie ist ihre verdeckte Voraussetzung.
Die Zeichengestalt verbraucht sich nicht im Gebrauch ihres Ereignisses. Der Modus der Wiederholung des Zeichens ist abstrakt und gründet sich auf der Abwesenheit des Subjekts und der Annahme der Unendlichkeit der Ressourcen (Raum, Zeit, Materie).
[...]
Der Alphabetismus findet in seiner letztlichen Digitalität und Linearität multimedial zu sich selbst und zu seinem Abschluß in der Objektivation seiner vermeintlichen Vernetzung. Die Graphematik be-wegt den Übergang der Inskription zur Ermöglichung einer nach-schriftlichen und trans-terrestrischen Epoche des Welt-Spiels.
Kaehr, Proömik und Disseminatorik, 1995
Translation
Thinking is realizing itself in the medium of the use of signs. Semiotics as the formalized theory of rational use of signs knows only the abstract linkage (concatenation/substitution) of given signs (finite or infinite) of a sign repertoire, which however can be formally reduced to two elements (atomic sign and blank) only.
In thinking, the sign as sign type carries itself due to the carry function of the materiality of the event of sign tokens. The difference of sign type and sign token (occurrence) itself is not reflected in semiotics; it is its covered condition.
The sign type does not use (consume) itself in the use of its event. The mode of iterability of the signs is abstract and based on the absence of subjectivity and the assumption of the infinity of resources (space, time, matter).
About sign systems
Elementary signs
„Elementary signs are signs that we shall consider as not having parts. The content of this concept depends upon the conventions that are assumed. [..] In simultanous consideration of any two elementary signs, we determine whether they are the same or different. These concepts are also conditional."
Abstraction of identification
"The possibility of determining when two elementary signs are the same permits us, applying an abstraction of identification, to speak of two identical elementary signs or of one and the same elementary sign. On this basis, we introduce the concept of an abstract elementary sign, that is, of an elementary sign, considered up to identity.
Concrete elementary signs will be considered as representatives of the corresponding abstract elementary signs. Two concrete elementary signs represent one and the same abstract elementary sign if and only if they are identical."
Abstract alphabets
"Lists of elementary signs are called alphabets. We shall call two alphabets equal if every elementary sign appearing in the first alphabet is identical with a certain elementary sign appearing in the second alphabet, and conversely. Alphabets considered up to equality will be called abstract alphabets."
Potential realizability
"Another abstraction, (...), is abstraction of potential realizability. This consists in departing from real limits of our constructive possibilities and beginning to discuss arbitrarily long abstract words as if they were constructible. Their realizability is potential: their representatives could be practically realized if we had at our disposal sufficient time, space, and materials." A. A. Markov
Ideality of Notational Systems
The abstractness of sign systems and their independence of real world conditions like space and matter, are brought one step further by Alfred Goguen’s definition of institutions and signatures for programming languages.
To speak about alphabetism in formal systems, with its atomicity, linearity, iterability, and ideality is not forgetting the conceptual move from alphabets as sign repertoires to the more abstract, category theoretic concept of signatures of institutions.
"Institutions accomplish this formalization by passing from "vocabularies" to signatures, which are abstract objects, and from "translations among vocabularies" to abstract mappings between objects, called signature morphisms;
then the parameterization of sentences by signatures is given by as assignment of a set Sen(S) of sentences to each signature S, and a translation Sen(f) from Sen(S) to Sen(S') for each signature morphism f: S –-> S', while the parameterization of models by signatures is given by an assignment of a class Mod(S) of models for each signature S, and a translation Mod(S') –-> Mod(S) for each f: S –-> S'.
[...]
Satisfaction is then a parameterized relation |=S between Mod(S) and Sen(S), such that the following satisfaction condition holds, for any signature morphism f: S –-> S', any S-model M, and any S'-sentence e: M |=S f(e) iff f(M) |=S' e
This condition expresses the invariance of truth under change of notation."
http://www.cs.ucsd.edu/users/goguen/projs/inst.html
Signatures are even better realizing alphabetism than sign repertoires because they are emphasizing the abstractness of alphabetical signs, that is, the ideality of signs, and sign systems, in contrast to the concrete occurrence of signs, independent of the content of the sign repertoire, i.e., the concrete notational material. Sign systems are not only characterized by atomicity, linearity, iterability, but also by ideality. Ideality is the medium of the realization of signs.
Uniqueness of Semiotics
Despite the fact that semiotics, like institutions, have many realizations, they are conceived as being conceptually unique. There is, in principle, one and only one semiotics. As there is, in principle, one and only one (u
niversal) logic. There may be many different semiotic or logical systems realizing special purposes.In the conceptual graph, uniqueness (oneness) is marked as 1. The trichotomy of semiotics is ruled by the order relations between alphabet (signature), rules (morphisms) and semiotics (institution) based on 1.
The oneness of semiotics has its foundation in mono-contexturality as opposed to poly-contexturality.
Negative Ecology
Today, we have to consider the destructiveness of sign systems. Technology, as realized in computing, is based on a sign-economy which is denying the limitations of its resources. By the application to real-world problems of understanding, organizing and computation, the abstractness of sign systems has become, after its deliberating function to human society, more and more an ecologically exploitative and destructive power. This might be a historical situation and might not to be the final paradigm of scriptural work. New notational systems, beyond alphabetism and not based on uniqueness, have to be invented.
Monday, September 04, 2006
On Chinese Mathematics
"Chinese culture lack formalization system like as Euclidean geometry, the circumstance disadvantages modernization of Chinese sciences, as well as modernization of technology and industry. The role of Combinatorics in the age of computer-web-information is the same as the role of Euclidean geometry in Industrialization. According to Constructivism mathematics, we believe and accept one mathematical object does exist if and only if we can construct it or build it in practice. So only parts of knowledge that have devised from manipulating the integers are truthfully reliable! " Steve Han (Jinan, ShanDong)
http://hanxianping.blogchina.com/886414.html
Magic Square in Lo Shu
(1)."Magic Square occurred in Lo Shu of the ancient China.
I think that represents the core of Chinese culture: Constructivism, Combinatorics. But they never become main stream culture in China." Steve Han
The story of 'Lo Shu' is as follows:
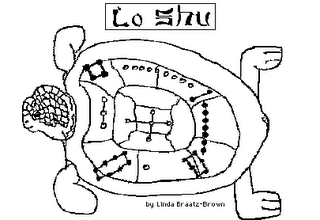
http://mathforum.org/alejandre/magic.square/loshu.html
In Chinese, the square is known as Luo Shu (Simplified Chinese: 洛书; Traditional Chinese: 洛書; pinyin: luò shū; Literal: Luo (River) Book) or the Nine Halls Diagram (Simplified Chinese: 九宫图; Traditional Chinese: 九宮圖; pinyin: jiǔ gōng tú).
http://en.wikipedia.org/wiki/Lo_Shu_Square
Magic Square
A magic square is a square array of numbers consisting of the distinct positive integers 1, 2, ..., n^2 arranged such that the sum of the n numbers in any horizontal, vertical, or main diagonal line is always the same number (Kraitchik 1952, p. 142; Andrews 1960, p. 1; Gardner 1961, p. 130; Madachy 1979).
Lo Shu is an associative magic square, but not a panmagic square.
(enter: Latin Square, Panmagic Square, associative Magic Square)
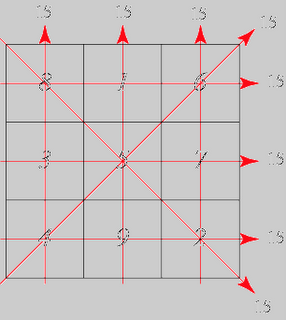
http://mathworld.wolfram.com/MagicSquare.html
Chinese vs. Greek mathematics
The first thing to understand about ancient Chinese mathematics is the way in which it differs from Greek mathematics. Unlike Greek mathematics there is no axiomatic development of mathematics. The Chinese concept of mathematical proof is radically different from that of the Greeks, yet one must not in any sense think less of it because of this. Rather one must marvel at the Chinese approach to mathematics and the results to which it led.
Chinese mathematics was, like their language, very concise. It was very much problem based, motivated by problems of the calendar, trade, land measurement, architecture, government records and taxes. By the fourth century BC counting boards were used for calculating, which effectively meant that a decimal place valued number system was in use. It is worth noting that counting boards are uniquely Chinese, and do not appear to have been used by any other civilization.
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Chinese_overview.html
Axiomatic Method
Chinese mathematicians didn't develop axiomatic methods like the Euclidean axioms of geometry. It seems, that this, too, was based on a clear decision and not on a lack of mathematizing ingenuity. Chinese mathematicians had been introduced to Euclid by Westerners. They liked the concise presentation of the topics but didn't think to adopt it to their own methods.
The axiomatic method, as developed by Euclid, is based on the evidence into the "eternal" truth of the axioms and the uniqueness of the rules of deduction. Aristotle has given in his Metaphysics a decisive philosophical justification of this world-view. He defended it against the more mythological approach of the Pythagoreans which promoted a multi-dimensional number theory.
Only after Riemann's multi-dimensional geometry and, finaly, by the Limitation Theorems of Kurt Godel, this belief system was radically questioned.
Interestingly, in the 20th century China developed important work for automatic proof systems for geometry. While the West was more interested in automatic proof systems for logical systems.
Art of Calculation
(2). "Chinese mathematical tradition is algorithmic." Steve Han
Chinese mathematics, was defined by Chinese in ancient times as the "art of calculation" (suan chu). This art was both a practical and spiritual one, and covered a wide range of subjects from religion and astronomy to water control and administration.
http://www.crystalinks.com/chinamath.html
In the West we are taught that the real difference between mathematics as an art of calculation and as a science started with the Greek mathematicians which contemplated numeric attributes not recognized by Babylonian-Egyptian mathematics, which remained on the level of an art&craft. Only with such an insight, independent on practical interests, like at first, into the difference of even and odd numbers and their attributes for further manipulations, mathematics as a scientific theory was established.
But a first glance at the Lo Shu shows, that the distinction of even and odd numbers was recognized and used for practical and theoretical reasons long before.
The Metaphor of Lo Shu
The Lo Shu Story is very interesting! I think it supports very much my ideas about the relationship of Chinese writing (logograms) and the design of new mathematics, maybe based on Morphogrammatics.
The metaphor of Lo Shu seems to confirm that Chinese math is radically different from Greek math as we know it in Western mathematics.
1. First it is in a written form, thus it has to be read (and not heard), i.e., it has to be deciphered and this knowledge has to be translated into sentences, i.e., into spoken language and then interpreted.
2. This procedure is not happening to a single Genius, like a Eureka insight, happening in the mind and then translated into spoken language and from there to an inscribed and written form. What happens with Lo Shu is a societal, co-operative and negotiating interpretation of the inscription on the back of the turtle which has to be discovered.
2. It is practical. The calculation which happens after the "child", i.e., a member of the population, not a Genius, discovered the signs on the turtle, i.e., the magic square, is practical (and mythical, sacrifice for the river-god) bridging the gap between culture and nature to stop the flooding.
3. Thus, the sign on the turtle is in fact not a sign but a topological logogram (morphogram), a tabular matrix, a mathematical inscription. But there is no need to identify such a tabular inscribtion with the modern mathematical concept of a matrix.
4. The problem inscribed on the turtle is purely combinatorial, and not in any sense logical, or sentence-based. It is in this sense not a riddle. Also not pronounced by an Oracle, offered to the scholars to interpretation.
5. The "truth" of the Square is given by a the reading (collecting) of it from all possible points of view, i.e., from all positions of the counting process, the sum has to be the same, which is 15. This process is generating an invariance principle as the form of truth.
6. The way of the counting, represented by the chain of numbers, is for all positions different. Each point of view has its own history and rationality.
7. The final result, the number 15, is not depending on the view-points, but is invariant of the single approaches. It is producing a collective mediation of the different positions, and at once generating societal collectivity. Also it appears as a final result, 15, the number is complex by the history of its construction. Each position has its own number 15. But a single result wouldn't convince the river-god. The convincing result is the collective number 15 as a result of mediation.
8. To each position, point of view, a singular number system can be attributed. Thus the result can be seen as a mediation, harmony, of different number systems. There is no information involved which would demand a unique number system like the modern linear arithmetic of natural numbers.
9. Also it is connected with numbers, the numbers are placed in a tabular order, square, grid, matrix and not linearly as a singular succession. The numbers are marked as patterns. Despite the strict positionality of the numbers, there is no zero sign involved.
There are many more interesting aspects in the story, like the fact that the turtle-matrix gives access to Nature. Thus, the writing is a bridge between human culture and nature. The turtle is considered as celestial. It is also producing time, societal time of the people involved. It is local, a gift for the specific river-god, but connected with a global cosmic insight. The Lo Shu is mediating local and global thematizations.
With this grammatological approach, I tried to avoid to map the Magic Square of Lo Shu to Western binary digitalism and arithmetic as it is usual today. Thus, in strict mathematical terms, the Lo Shu is not a Magic Square. Simply because it is not a mathematical matrix based on natural numbers. Such an interpretation of Lo Shu as a Magic Square is denying its specific Ancient concept of Numbers. This may have far reaching consequences in the context of interpretations of I Ching, Trigrams, Feng Shui and Yin&Yang.
Chinese culture: Constructivism
Constructivism, in the West, is based on mathematical constructivism in the sense of Brouwer and Heyting. It is totally different from the Chines Constructivism as suggested by the Turtle Metaphor. Western constructivism is based on a solitaire, mental, subjective insight in the nature of Numbers. It is based on subjective intuition. Only later, as a second step, the intuitions have to be written down; down from the mind to the paper. Today, to a computer program.
Therefore, Western constructivism lacks all the characteristics mentioned above: written, societal, negotiable, practical, combinatorial, tabular, dynamic, etc.
Constructivism in Western philosophy and cybernetics (Second-Order Cybernetics) is more speculative, involving some circularities, but is nevertheless very close to mathematical constructivism (intuitionism) and its problems with solipsism.
Constructivism, today, is very much supported by the needs of computer science.
http://hanxianping.blogchina.com/886414.html
Magic Square in Lo Shu
(1)."Magic Square occurred in Lo Shu of the ancient China.
I think that represents the core of Chinese culture: Constructivism, Combinatorics. But they never become main stream culture in China." Steve Han
The story of 'Lo Shu' is as follows:
In the ancient time of China, there was a huge flood.
The people tried to offer some sacrifice to the 'river god'
of one of the flooding rivers, the 'Lo' river, to calm his
anger. However, every time a turtle came from the river and
walked around the sacrifice. The river god didn't accept
the sacrifice until one time, a child noticed the curious
figure on the turtle shell. Hence they realized the correct
amount of sacrifice to make.
http://mathforum.org/alejandre/magic.square/loshu.html
Legends attribute China prehistoric personality, Hsia Yu (Lo Shu, "scroll of the river Lo", dating as early as 2800 BC.) - he who tamed the Yellow River of floods (
) to be the one who discovered the Lo Shu.
Yu saw some very interesting markings on the shell of a giant tortoise that emerged from the River Lo in Central China. This became Lo Shu.
http://www.hiakz.com/loshu.asp
In Chinese, the square is known as Luo Shu (Simplified Chinese: 洛书; Traditional Chinese: 洛書; pinyin: luò shū; Literal: Luo (River) Book) or the Nine Halls Diagram (Simplified Chinese: 九宫图; Traditional Chinese: 九宮圖; pinyin: jiǔ gōng tú).
http://en.wikipedia.org/wiki/Lo_Shu_Square
Magic Square
A magic square is a square array of numbers consisting of the distinct positive integers 1, 2, ..., n^2 arranged such that the sum of the n numbers in any horizontal, vertical, or main diagonal line is always the same number (Kraitchik 1952, p. 142; Andrews 1960, p. 1; Gardner 1961, p. 130; Madachy 1979).
Lo Shu is an associative magic square, but not a panmagic square.
(enter: Latin Square, Panmagic Square, associative Magic Square)
http://mathworld.wolfram.com/MagicSquare.html
Chinese vs. Greek mathematics
The first thing to understand about ancient Chinese mathematics is the way in which it differs from Greek mathematics. Unlike Greek mathematics there is no axiomatic development of mathematics. The Chinese concept of mathematical proof is radically different from that of the Greeks, yet one must not in any sense think less of it because of this. Rather one must marvel at the Chinese approach to mathematics and the results to which it led.
Chinese mathematics was, like their language, very concise. It was very much problem based, motivated by problems of the calendar, trade, land measurement, architecture, government records and taxes. By the fourth century BC counting boards were used for calculating, which effectively meant that a decimal place valued number system was in use. It is worth noting that counting boards are uniquely Chinese, and do not appear to have been used by any other civilization.
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Chinese_overview.html
Axiomatic Method
Chinese mathematicians didn't develop axiomatic methods like the Euclidean axioms of geometry. It seems, that this, too, was based on a clear decision and not on a lack of mathematizing ingenuity. Chinese mathematicians had been introduced to Euclid by Westerners. They liked the concise presentation of the topics but didn't think to adopt it to their own methods.
The axiomatic method, as developed by Euclid, is based on the evidence into the "eternal" truth of the axioms and the uniqueness of the rules of deduction. Aristotle has given in his Metaphysics a decisive philosophical justification of this world-view. He defended it against the more mythological approach of the Pythagoreans which promoted a multi-dimensional number theory.
Only after Riemann's multi-dimensional geometry and, finaly, by the Limitation Theorems of Kurt Godel, this belief system was radically questioned.
Interestingly, in the 20th century China developed important work for automatic proof systems for geometry. While the West was more interested in automatic proof systems for logical systems.
Art of Calculation
(2). "Chinese mathematical tradition is algorithmic." Steve Han
Chinese mathematics, was defined by Chinese in ancient times as the "art of calculation" (suan chu). This art was both a practical and spiritual one, and covered a wide range of subjects from religion and astronomy to water control and administration.
http://www.crystalinks.com/chinamath.html
In the West we are taught that the real difference between mathematics as an art of calculation and as a science started with the Greek mathematicians which contemplated numeric attributes not recognized by Babylonian-Egyptian mathematics, which remained on the level of an art&craft. Only with such an insight, independent on practical interests, like at first, into the difference of even and odd numbers and their attributes for further manipulations, mathematics as a scientific theory was established.
But a first glance at the Lo Shu shows, that the distinction of even and odd numbers was recognized and used for practical and theoretical reasons long before.
The Metaphor of Lo Shu
The Lo Shu Story is very interesting! I think it supports very much my ideas about the relationship of Chinese writing (logograms) and the design of new mathematics, maybe based on Morphogrammatics.
The metaphor of Lo Shu seems to confirm that Chinese math is radically different from Greek math as we know it in Western mathematics.
1. First it is in a written form, thus it has to be read (and not heard), i.e., it has to be deciphered and this knowledge has to be translated into sentences, i.e., into spoken language and then interpreted.
2. This procedure is not happening to a single Genius, like a Eureka insight, happening in the mind and then translated into spoken language and from there to an inscribed and written form. What happens with Lo Shu is a societal, co-operative and negotiating interpretation of the inscription on the back of the turtle which has to be discovered.
2. It is practical. The calculation which happens after the "child", i.e., a member of the population, not a Genius, discovered the signs on the turtle, i.e., the magic square, is practical (and mythical, sacrifice for the river-god) bridging the gap between culture and nature to stop the flooding.
3. Thus, the sign on the turtle is in fact not a sign but a topological logogram (morphogram), a tabular matrix, a mathematical inscription. But there is no need to identify such a tabular inscribtion with the modern mathematical concept of a matrix.
4. The problem inscribed on the turtle is purely combinatorial, and not in any sense logical, or sentence-based. It is in this sense not a riddle. Also not pronounced by an Oracle, offered to the scholars to interpretation.
5. The "truth" of the Square is given by a the reading (collecting) of it from all possible points of view, i.e., from all positions of the counting process, the sum has to be the same, which is 15. This process is generating an invariance principle as the form of truth.
6. The way of the counting, represented by the chain of numbers, is for all positions different. Each point of view has its own history and rationality.
7. The final result, the number 15, is not depending on the view-points, but is invariant of the single approaches. It is producing a collective mediation of the different positions, and at once generating societal collectivity. Also it appears as a final result, 15, the number is complex by the history of its construction. Each position has its own number 15. But a single result wouldn't convince the river-god. The convincing result is the collective number 15 as a result of mediation.
8. To each position, point of view, a singular number system can be attributed. Thus the result can be seen as a mediation, harmony, of different number systems. There is no information involved which would demand a unique number system like the modern linear arithmetic of natural numbers.
9. Also it is connected with numbers, the numbers are placed in a tabular order, square, grid, matrix and not linearly as a singular succession. The numbers are marked as patterns. Despite the strict positionality of the numbers, there is no zero sign involved.
There are many more interesting aspects in the story, like the fact that the turtle-matrix gives access to Nature. Thus, the writing is a bridge between human culture and nature. The turtle is considered as celestial. It is also producing time, societal time of the people involved. It is local, a gift for the specific river-god, but connected with a global cosmic insight. The Lo Shu is mediating local and global thematizations.
With this grammatological approach, I tried to avoid to map the Magic Square of Lo Shu to Western binary digitalism and arithmetic as it is usual today. Thus, in strict mathematical terms, the Lo Shu is not a Magic Square. Simply because it is not a mathematical matrix based on natural numbers. Such an interpretation of Lo Shu as a Magic Square is denying its specific Ancient concept of Numbers. This may have far reaching consequences in the context of interpretations of I Ching, Trigrams, Feng Shui and Yin&Yang.
Chinese culture: Constructivism
Constructivism, in the West, is based on mathematical constructivism in the sense of Brouwer and Heyting. It is totally different from the Chines Constructivism as suggested by the Turtle Metaphor. Western constructivism is based on a solitaire, mental, subjective insight in the nature of Numbers. It is based on subjective intuition. Only later, as a second step, the intuitions have to be written down; down from the mind to the paper. Today, to a computer program.
Therefore, Western constructivism lacks all the characteristics mentioned above: written, societal, negotiable, practical, combinatorial, tabular, dynamic, etc.
Constructivism in Western philosophy and cybernetics (Second-Order Cybernetics) is more speculative, involving some circularities, but is nevertheless very close to mathematical constructivism (intuitionism) and its problems with solipsism.
Constructivism, today, is very much supported by the needs of computer science.
Friday, September 01, 2006
《中国挑战：一个新猜想》
—— 对"中国挑战"说的一个注释
作者：Rudolf Kaehr
翻译：韩宪平/Steve Han
来源：思维实验室
网址：www.thinkartlab.com
"我们能从中国人没有教我们的地方学到什么？"——鲁道夫
主 流文化依赖于书写模式。民族的理性特质、他们的技术有效性、他们把社会组织起来、交流信息、以及他们的艺术科学等等这一切都跟书写模式分不开；人们在书 写和创建自己作为典籍的文化实践中学会思维和生活。主流文化总是依赖于某种书写里包含的理性和技术模式。一般来说，书写是一种文化、政治和技术形成的最抽 象的机制和技术（1）。
——欧洲的文化及第一次猜想
欧洲的文化依赖于字母书写和印度的零占位机制（2），这种机制使得算术、计算的经济合理、形式化和编程语言成为可能（3）。
莱 布尼茨提出第一个关于中国文字的猜想。他设想了一种"通用语言（4）"作为国家和人民之间沟通的可信赖的通信基础。他的这个想法类似于中国的象形文字， 中国象形文字通过典籍在不同口头语言之间起着桥梁作用。要实现这一梦想他发明了凝练的数字表示和计算系统，这就是二进制系统，依此作为欧洲对古老的中国" 易经（5）"的一个回应，最终他发明了独立于任何民族语言的运算方法和逻辑，还有作为计算机的原型的计算机器（6）。
现代欧洲科学技术遵循了莱布尼茨的想法，产生了技术上的二进制主义和数字主义，并形成了今天西方——以及亚洲——的基本技术和经济力量。但是，欧洲的技术力量停留在"老欧洲"的意识形态、形而上学和伦理学框架和限制当中。
——美国的美式梦想
在美国，欧洲的思维和技术形式摆脱了她的形而上学老套子，发明了"无所不在的计算"，实现了人工智能，人工生命，认知系统，机器人等等；实现了无限扩张的数字主义（7）。
今 天，美国的美式梦想气数已尽（8）！美式梦想的成功已经接近了尾声；而老欧洲还由她的古希腊起源支配着（9），摆脱了欧洲限制的美式梦想现在迷失了根 本，失掉了设计未来的精神源泉。美国的必然衰落是由于"无根"！与欧洲分道扬镳，成了无本之木无源之水，在数字主义达到了她的颠峰。在沉湎于"数字形而上 学"
中并归结为0和1的不朽精神世界中，展望更先进的科技发展似乎是不可能的了（10）。全部美国式发展会在"数字实用主义"世界观中固步自封！
所以，基于古希腊字母文字、印度的数论和莱布尼兹采用中国文字模型，这一切作为欧洲和美国的美式梦想失去了设计世界未来发展的力量。
——中国书写模式
中 国没有发展出类似的哲学（11）、科学（12）和技术（13），这是因为她的超复杂的书写模式，现在正在采用西方的科学技术成果；但是，中国在下一个时 代自有对西方的优势：有没有被开发的丰富典籍资源。中国文字永远是她的文化和政治的基础和保证，没有"字母线性主义"和数字主义的限制。西方思维的线性性 质是更容易映射进入中国理性的"表格样式"的。这种映射过程，在中国文字的自明性质方面不会导致任何混乱。
中国文字概念是表格样式的、多维度的、嵌入式的、开放的、复杂的和基于民族最古老文化传统的（14）。而这些特征正符合科学技术在处理现代社会问题和开创新未来的要求的。
因 此，为今而言，所谓中国的挑战，不是为西方视为危惧的新的经济实力和经济扩张（15），而是在作为未来技术革命基础的中国理性重新发现的可能性方面。中 国理性把任何美国式的东西远远地甩在了后面。中国对西方的挑战不是经济的、也不是政治的或者军事的；苏醒的技术中国和经济中国这个事件并不构成对西方的所 谓的"大挑战"，真正的挑战是重新发现她的文字系统，并设计出新的理性形式系统，就像创造新的数学和新的编程语言一样（16）；是面对一个崛起的中国我们 是否做好了充分的准备。
因为忙于适应西方的技术和经济，中国官方还没有意识到这种形成未来主流文化基础的可能性。可能吧，十九世纪是欧洲世纪，二十世纪是美国世纪，而二十一世纪将是中国世纪。
——形态语法学：第二个猜想
我 的想法作为后欧洲的第二个关于中国文字的猜想由此而生。第一步，我提出"多结构逻辑（Polycontextural Logic）（17）"的研究和"形态语法学（Morphogrammtics）（18）"研究，作为在西方模式走到尽头时，对中国理性和技术的概念系统 作的一个可能的、新的理解。这一工作——我知道它的风险——是某种实验性的猜想，具有永恒自解构的能力，超越西方、亚洲在思维和技术方面的"具象中心主义 （19）"，形而上学的单一结构主义（20）。
形态语法学和多结构理论包含并且超越西方的思维、计算和编程语言的设计，能够满足新时代对操作理性提出的表格样式（21）的处理和对复杂性处理的要求。
猜想总是文化传统革命的前奏，总是为文化管理者所拒绝。
参考资源
1. enter: Gotthard Gunther, Villem Flusser, Arnold Gehlen, McLuhan
2. http://saxakali.com/COLOR_ASP/discoverof0.htm
http://www-history.mcs.st-and.ac.uk/HistTopics/Zero.html
http://home.ubalt.edu/ntsbarsh/zero/ZERO.HTM
3. http://www.csee.umbc.edu/help/theory/lang_def.shtml
4. http://en.wikipedia.org/wiki/Gottfried_Leibniz
5. http://www.kirjasto.sci.fi/leibnitz.htm
6. http://www.idsia.ch/~juergen/leibniz.html
7. Mark Weiser: http://www.ubiq.com/hypertext/weiser/UbiHome.html
8.
http://www.the-american-interest.com/cms/contents.cfm
http://www.the-american-interest.com/cms/joffe.cfm
http://www.kath.de/internet/vortrag/mueller_technospiritualitaet_vortrag.pdf
http://www.transnational.org/forum/meet/2004/Galtung_USempireFall.html
9.
http://www.spiked-online.com/index.php?/surveys/2024_article/1310/
http://www.nesc.ac.uk/esi/events/Grand_Challenges/
10. http://roundtable.kein.org/node/414
Moravec, H. (1988), Mind Children: The Future of Robot and Human Intelligence.
http://www.metanexus.net/metanexus_online/show_article2.asp?id=9115
enter: Ed Fredkin, Stephen Wolfram, Holtzman
http://digitalphilosophy.org/on_the_soul.htm
11. http://plato.stanford.edu/entries/comparphil-chiwes/#1
12. http://www.formalontology.it/chinese-philosophy.htm
http://saxakali.com/COLOR_ASP/chinamh1.htm
13. http://hanxianping.blogchina.com/886414.html
14. http://news.xinhuanet.com/english/2006-03/28/content_4356764.htm
15. Andrew Neil, What China can teach the West
http://www.thebusinessonline.com/Stories.aspx?StoryId=04007447-420D-41B3-ADC3-338E68C0F5EC&page=0
16. Han-liang Chang, Hallucinating the Other: Derridean Fantasies of Chinese Script
http://www.lttc.ntu.edu.tw/academics/changhl/hallucinating.pdf
17. http://www.thinkartlab.com/pkl/lola/PolyLogics.pdf
18. http://www.thinkartlab.com/pkl/tm/MG-Buch.pdf
19. Archive for Derrida and Deconstructivism: http://www.hydra.umn.edu/derrida/
20. www.thinkartlab.com/pkl/media/SUSHIS_LOGICS.pdf
21. Gotthard Gunther: http://www.thinkartlab.com/pkl/archive/Cyberphilosophy.pdf
作者：Rudolf Kaehr
翻译：韩宪平/Steve Han
来源：思维实验室
网址：www.thinkartlab.com
"我们能从中国人没有教我们的地方学到什么？"——鲁道夫
主 流文化依赖于书写模式。民族的理性特质、他们的技术有效性、他们把社会组织起来、交流信息、以及他们的艺术科学等等这一切都跟书写模式分不开；人们在书 写和创建自己作为典籍的文化实践中学会思维和生活。主流文化总是依赖于某种书写里包含的理性和技术模式。一般来说，书写是一种文化、政治和技术形成的最抽 象的机制和技术（1）。
——欧洲的文化及第一次猜想
欧洲的文化依赖于字母书写和印度的零占位机制（2），这种机制使得算术、计算的经济合理、形式化和编程语言成为可能（3）。
莱 布尼茨提出第一个关于中国文字的猜想。他设想了一种"通用语言（4）"作为国家和人民之间沟通的可信赖的通信基础。他的这个想法类似于中国的象形文字， 中国象形文字通过典籍在不同口头语言之间起着桥梁作用。要实现这一梦想他发明了凝练的数字表示和计算系统，这就是二进制系统，依此作为欧洲对古老的中国" 易经（5）"的一个回应，最终他发明了独立于任何民族语言的运算方法和逻辑，还有作为计算机的原型的计算机器（6）。
现代欧洲科学技术遵循了莱布尼茨的想法，产生了技术上的二进制主义和数字主义，并形成了今天西方——以及亚洲——的基本技术和经济力量。但是，欧洲的技术力量停留在"老欧洲"的意识形态、形而上学和伦理学框架和限制当中。
——美国的美式梦想
在美国，欧洲的思维和技术形式摆脱了她的形而上学老套子，发明了"无所不在的计算"，实现了人工智能，人工生命，认知系统，机器人等等；实现了无限扩张的数字主义（7）。
今 天，美国的美式梦想气数已尽（8）！美式梦想的成功已经接近了尾声；而老欧洲还由她的古希腊起源支配着（9），摆脱了欧洲限制的美式梦想现在迷失了根 本，失掉了设计未来的精神源泉。美国的必然衰落是由于"无根"！与欧洲分道扬镳，成了无本之木无源之水，在数字主义达到了她的颠峰。在沉湎于"数字形而上 学"
中并归结为0和1的不朽精神世界中，展望更先进的科技发展似乎是不可能的了（10）。全部美国式发展会在"数字实用主义"世界观中固步自封！
所以，基于古希腊字母文字、印度的数论和莱布尼兹采用中国文字模型，这一切作为欧洲和美国的美式梦想失去了设计世界未来发展的力量。
——中国书写模式
中 国没有发展出类似的哲学（11）、科学（12）和技术（13），这是因为她的超复杂的书写模式，现在正在采用西方的科学技术成果；但是，中国在下一个时 代自有对西方的优势：有没有被开发的丰富典籍资源。中国文字永远是她的文化和政治的基础和保证，没有"字母线性主义"和数字主义的限制。西方思维的线性性 质是更容易映射进入中国理性的"表格样式"的。这种映射过程，在中国文字的自明性质方面不会导致任何混乱。
中国文字概念是表格样式的、多维度的、嵌入式的、开放的、复杂的和基于民族最古老文化传统的（14）。而这些特征正符合科学技术在处理现代社会问题和开创新未来的要求的。
因 此，为今而言，所谓中国的挑战，不是为西方视为危惧的新的经济实力和经济扩张（15），而是在作为未来技术革命基础的中国理性重新发现的可能性方面。中 国理性把任何美国式的东西远远地甩在了后面。中国对西方的挑战不是经济的、也不是政治的或者军事的；苏醒的技术中国和经济中国这个事件并不构成对西方的所 谓的"大挑战"，真正的挑战是重新发现她的文字系统，并设计出新的理性形式系统，就像创造新的数学和新的编程语言一样（16）；是面对一个崛起的中国我们 是否做好了充分的准备。
因为忙于适应西方的技术和经济，中国官方还没有意识到这种形成未来主流文化基础的可能性。可能吧，十九世纪是欧洲世纪，二十世纪是美国世纪，而二十一世纪将是中国世纪。
——形态语法学：第二个猜想
我 的想法作为后欧洲的第二个关于中国文字的猜想由此而生。第一步，我提出"多结构逻辑（Polycontextural Logic）（17）"的研究和"形态语法学（Morphogrammtics）（18）"研究，作为在西方模式走到尽头时，对中国理性和技术的概念系统 作的一个可能的、新的理解。这一工作——我知道它的风险——是某种实验性的猜想，具有永恒自解构的能力，超越西方、亚洲在思维和技术方面的"具象中心主义 （19）"，形而上学的单一结构主义（20）。
形态语法学和多结构理论包含并且超越西方的思维、计算和编程语言的设计，能够满足新时代对操作理性提出的表格样式（21）的处理和对复杂性处理的要求。
猜想总是文化传统革命的前奏，总是为文化管理者所拒绝。
参考资源
1. enter: Gotthard Gunther, Villem Flusser, Arnold Gehlen, McLuhan
2. http://saxakali.com/COLOR_ASP/discoverof0.htm
http://www-history.mcs.st-and.ac.uk/HistTopics/Zero.html
http://home.ubalt.edu/ntsbarsh/zero/ZERO.HTM
3. http://www.csee.umbc.edu/help/theory/lang_def.shtml
4. http://en.wikipedia.org/wiki/Gottfried_Leibniz
5. http://www.kirjasto.sci.fi/leibnitz.htm
6. http://www.idsia.ch/~juergen/leibniz.html
7. Mark Weiser: http://www.ubiq.com/hypertext/weiser/UbiHome.html
8.
http://www.the-american-interest.com/cms/contents.cfm
http://www.the-american-interest.com/cms/joffe.cfm
http://www.kath.de/internet/vortrag/mueller_technospiritualitaet_vortrag.pdf
http://www.transnational.org/forum/meet/2004/Galtung_USempireFall.html
9.
http://www.spiked-online.com/index.php?/surveys/2024_article/1310/
http://www.nesc.ac.uk/esi/events/Grand_Challenges/
10. http://roundtable.kein.org/node/414
Moravec, H. (1988), Mind Children: The Future of Robot and Human Intelligence.
http://www.metanexus.net/metanexus_online/show_article2.asp?id=9115
enter: Ed Fredkin, Stephen Wolfram, Holtzman
http://digitalphilosophy.org/on_the_soul.htm
11. http://plato.stanford.edu/entries/comparphil-chiwes/#1
12. http://www.formalontology.it/chinese-philosophy.htm
http://saxakali.com/COLOR_ASP/chinamh1.htm
13. http://hanxianping.blogchina.com/886414.html
14. http://news.xinhuanet.com/english/2006-03/28/content_4356764.htm
15. Andrew Neil, What China can teach the West
http://www.thebusinessonline.com/Stories.aspx?StoryId=04007447-420D-41B3-ADC3-338E68C0F5EC&page=0
16. Han-liang Chang, Hallucinating the Other: Derridean Fantasies of Chinese Script
http://www.lttc.ntu.edu.tw/academics/changhl/hallucinating.pdf
17. http://www.thinkartlab.com/pkl/lola/PolyLogics.pdf
18. http://www.thinkartlab.com/pkl/tm/MG-Buch.pdf
19. Archive for Derrida and Deconstructivism: http://www.hydra.umn.edu/derrida/
20. www.thinkartlab.com/pkl/media/SUSHIS_LOGICS.pdf
21. Gotthard Gunther: http://www.thinkartlab.com/pkl/archive/Cyberphilosophy.pdf
Subscribe to:
Posts (Atom)